Let us learn what are Triangle inequalities,
You have just seen that if a triangle has equal sides, the angles opposite these sides are equal, and if a triangle has equal angles, the sides opposite these angles are equal. There are two important theorems involving unequal sides and unequal angles in triangles. They are:
Theorem: If two sides of a triangle are unequal, then the measures of the angles opposite these sides are unequal, and the greater angle is opposite the greater side.
Theorem: If two angles of a triangle are unequal, then the measures of the sides opposite these angles are also unequal, and the longer side is opposite the greater angle.
Example : Figure 1 shows a triangle with angles of different measures. List the sides of this triangle in order from least to greatest.
 Figure : List the sides of this triangle in increasing order.
Figure : List the sides of this triangle in increasing order.
Because 30° < 50° < 100°, then RS < QR < QS.
You have just seen that if a triangle has equal sides, the angles opposite these sides are equal, and if a triangle has equal angles, the sides opposite these angles are equal. There are two important theorems involving unequal sides and unequal angles in triangles. They are:
Theorem: If two sides of a triangle are unequal, then the measures of the angles opposite these sides are unequal, and the greater angle is opposite the greater side.
Theorem: If two angles of a triangle are unequal, then the measures of the sides opposite these angles are also unequal, and the longer side is opposite the greater angle.
Example : Figure 1 shows a triangle with angles of different measures. List the sides of this triangle in order from least to greatest.
 Figure : List the sides of this triangle in increasing order.
Figure : List the sides of this triangle in increasing order.Because 30° < 50° < 100°, then RS < QR < QS.
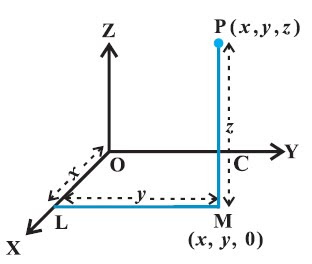 Let us learn about Coordinates of a Point in Space,
Let us learn about Coordinates of a Point in Space,
