Welcome to free math tutor,
If you've graphed equations, look at the graph
of y=1/x. If you look at the region enclosed by y=1/x, the line y=0 (the
x-axis), and the lines x=1 and x=e, it looks like a rectangle but with one
curved side. What is the area of this shape? In fact, it is exactly 1. examples on math help;
Mathematically speaking, we say "the area under the curve y=1/x from 1 to e
is 1," or even better, "the *integral* of 1/x from 1 to e is 1." This is
because if we replaced the line x=e with some line x=b for some b>1, the
area of the region is the natural logarithm of b.
Note the natural logarithm
of e is 1, because e^1 = e; that is, 1 is the exponent for which the base
(e) is equal to e.
And finally, for something I hope someone else will explain,
e^(i*Pi) = -1, where i is the square root of -1.
If you've graphed equations, look at the graph
of y=1/x. If you look at the region enclosed by y=1/x, the line y=0 (the
x-axis), and the lines x=1 and x=e, it looks like a rectangle but with one
curved side. What is the area of this shape? In fact, it is exactly 1. examples on math help;
Mathematically speaking, we say "the area under the curve y=1/x from 1 to e
is 1," or even better, "the *integral* of 1/x from 1 to e is 1." This is
because if we replaced the line x=e with some line x=b for some b>1, the
area of the region is the natural logarithm of b.
Note the natural logarithm
of e is 1, because e^1 = e; that is, 1 is the exponent for which the base
(e) is equal to e.
And finally, for something I hope someone else will explain,
e^(i*Pi) = -1, where i is the square root of -1.









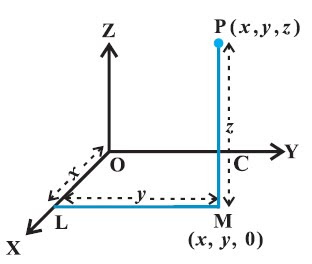 Let us learn about Coordinates of a Point in Space,
Let us learn about Coordinates of a Point in Space,