Polynomials
Introduction:
A Polynomial is an expression of finite length constructed from variables (also known as indeterminates).We can generally find polonomials in a wide variety and a wide range.For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated problems in the sciences; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science.
A polynomial is either zero, or can be written as the sum of one or more non-zero terms. The number of terms is finite. These terms consist of a constant (called the coefficient of the term) which may be multiplied by a finite number of variables (usually represented by letters). Each variable may have an exponent that is a non-negative integer, i.e., a natural number. The exponent on a variable in a term is called the degree of that variable in that term, the degree of the term is the sum of the degrees of the variables in that term, and the degree of a polynomial is the largest degree of any one term. Since x = x1, the degree of a variable without a written exponent is one. A term with no variables is called a constant term, or just a constant.
A polynomial function is a function that can be defined by evaluating a polynomial. A function ƒ of one argument is called a polynomial function if it satisfies
A polynomial equation is an equation in which a polynomial is set equal to another polynomial.
Introduction:
A Polynomial is an expression of finite length constructed from variables (also known as indeterminates).We can generally find polonomials in a wide variety and a wide range.For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated problems in the sciences; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science.
A polynomial is either zero, or can be written as the sum of one or more non-zero terms. The number of terms is finite. These terms consist of a constant (called the coefficient of the term) which may be multiplied by a finite number of variables (usually represented by letters). Each variable may have an exponent that is a non-negative integer, i.e., a natural number. The exponent on a variable in a term is called the degree of that variable in that term, the degree of the term is the sum of the degrees of the variables in that term, and the degree of a polynomial is the largest degree of any one term. Since x = x1, the degree of a variable without a written exponent is one. A term with no variables is called a constant term, or just a constant.
A polynomial is a sum of terms:
For example, the following is a polynomial: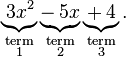
- Now lets learn about:Polynomial Functions:
Polynomial Functions:
A polynomial function is a function that can be defined by evaluating a polynomial. A function ƒ of one argument is called a polynomial function if it satisfies
Polynomial Equation:
A polynomial equation is an equation in which a polynomial is set equal to another polynomial.

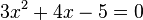
No comments:
Post a Comment